3 Planes That Intersect In One Line
This systems solution will be. Similarly one can specify a plane in 3-space by giving its inclination and one of its points.

Solving Systems Of Three Equations In Three Variables Precalculus I
In this video we look at a common exercise where we are asked to find the line of intersection of two planes in space.
3 planes that intersect in one line. When you know two points in the intersection of two planes Postulates 1-1 and 1-3 tell you that the line through those points is the line of intersection of the planes. For example 2x y - 3z 4is a translation of 2x y - 3z 0. 4x 2y 2z 6 0.
The intersection of the three planes is a line. Because the point on the intersection line must also be in both planes lets set z 0 so well be in the xy-plane in both of the equations of our planes. All three planes are parallel.
The intersection line between two planes passes throught the points 10-2 and 1-23 We also know that the point 24-5is located on the planefind the equation of the given plan and the equation of another plane with a tilted by 60 degree to the given plane and has the same intersection line given for the first plane. The line and the plane do not intersect There are no solutions. It doesnt have to intersect all three of the coordinate planes but it will have to intersect at least one.
Can I do 3 2 to get the line 6 y 15 z 6 and 1 2 to get the line 2 y 5 z 1 which is 6 y 15 z 3 and say that as these. The first and second are coincident and the third is parallel to them. Heres a Python example which finds the intersection of a line and a plane.
Step 2 Draw a second plane that is horizontal. Ö Two planes are coincident and the third plane is not parallel to the coincident planes. This is thoroughly answered here.
Shade this plane a different color. To show whether or not the 3 planes. A Plane and a point intersect.
Yes there are three ways that two different planes can intersect a line. 2x y z 2 0. The line and the plane intersect at a single point There is exactly one solution.
01 Lines and Planes in 3-space Planes in 3-space In Geometry a line in 2-space can be identifled through its slope and one of its points. Now click the circle in the left menu to make the blue plane reappear. 2x y z 3 0.
1 2 3 2 9 1 2 9 33. Whatever our line of intersection is it must intersect at least one of the coordinate planes. Any three points _determine a plane.
The coefficients ABCDare proportional for these two equations. If we found in nitely many solutions the lines are the same. So if the null space has dimension 1 this means the three planes corresponding to 0s on their right sides intersect in a line.
1 Both planes intersect each other and their intersection forms the line in the system. Next we nd the direction vector d for the line of intersection by computing d n 1 n 2 2 4 1 5 3 3 5 2 3 2 2 3 2 5 2 32 3 3 1 2 12 5 3 3 2 4 7 13 3. The normal vector n 1 of x 1 5x 2 3x 3 11 is 2 4 1 5 3 3 5 and the normal vector n 2 of 3x 1 2x 2 2x 3 7 is 2 4 3 2 2 3 5.
Use dashed lines to show where one plane is hidden. Ö Two scalar equations are equivalent. MMonitoring Progressonitoring Progress Help in English and Spanish at.
Ö The intersection is a line. Then deselect the green red planes by clicking on the corresponding circles in the left menu. Step 3 Draw the line of intersection.
If a line and a plane intersect one another the intersection will either be a single point or a line if the line lies in the plane. Find the equation of the plane that contains the point 130 and the line given by x 3 2t y 4t z 7 t. Examples Example 2 Use Gaussian elimination to determine all points of intersection of the following three planes.
Bookmark this question. Two points determine a line. Three planes are parallel but not coincident all three planes form a cluster of planes intersecting in one common line a sheaf all three planes form a prism the three planes intersect in a single point.
All have a common line of intersection. Recall that given a line and a plane in IR3 there are three possibilities for the intersection of the line with the plane The line is parallel to the plane orthogonal to a normal vector of the plane. Where the plane can be either a point and a normal or a 4d vector normal form In the examples below code for both is provided.
Two planes intersect in a line 5. 2 x y 3 z 6. If two planes intersect each other the curve of intersection will always be a line.
For indicating the inclination it is convenient to report a vector which is orthogonal to the plane. A line and a point intersect. The idea is as follows.
Line Intersection Two Coincident Planes and one Intersecting Plane In this case. O y x y 2x and plane 8 y 3x 7 1 3 2 3 2 57 4 4 2 postulate axiom 12 Basic Postulates of Geometry Key Concepts. The normal vector of the second plane n2 4 1 3 is not parallel to either of these so the second plane must intersect each of the other two planes in a line This situation is drawn here.
3 x 5 y 12 z 12. First we read o the normal vectors of the planes. Lots of options to start.
Also note that this function calculates a value representing where the point is on the line called fac in the code below. Now that the two planes are hidden observe how the line of intersection between the green and red planes the black line intersects the blue plane. To find the symmetric equations that represent that intersection line youll need the cross product of the normal vectors of the two planes as well as a point on the line of intersection.
3 11 and 3x 1 2x 2 2x 3 7. To find the intersection of the line and the plane we usually start by expressing the line as a set of parametric equations and the plane in the standard form for the equation of a plane. Just two planes are parallel and the 3rd plane cuts each in a line.
The lines intersect at a point. Show activity on this post. Any three points not on the same line determine a plane.
Investigate the intersection values between the three planes. There is a similar postulate about the intersection of planes. A line has endpoints.
SOLUTION Step 1 Draw a vertical plane. Each plane ax by cz dis just a translation of the plane ax by cz 0. As long as the two planes are not para.
If we found no solution then the lines dont intersect. You may want to return this too because values from 0 to 1. We know a point on the line is 13.
The intersection of the three planes is a point. Sketch two planes that intersect in a line. 3 on a question.
The second and third planes are coincident and the first is cuting them therefore the three planes intersect in a line. So lets see if it intersects the xy-plane. In 3D three planes and can intersect or not in the following ways.
1 x y 2 z 5.

Lesson 84 Intersection Of 3 Planes Ppt Download
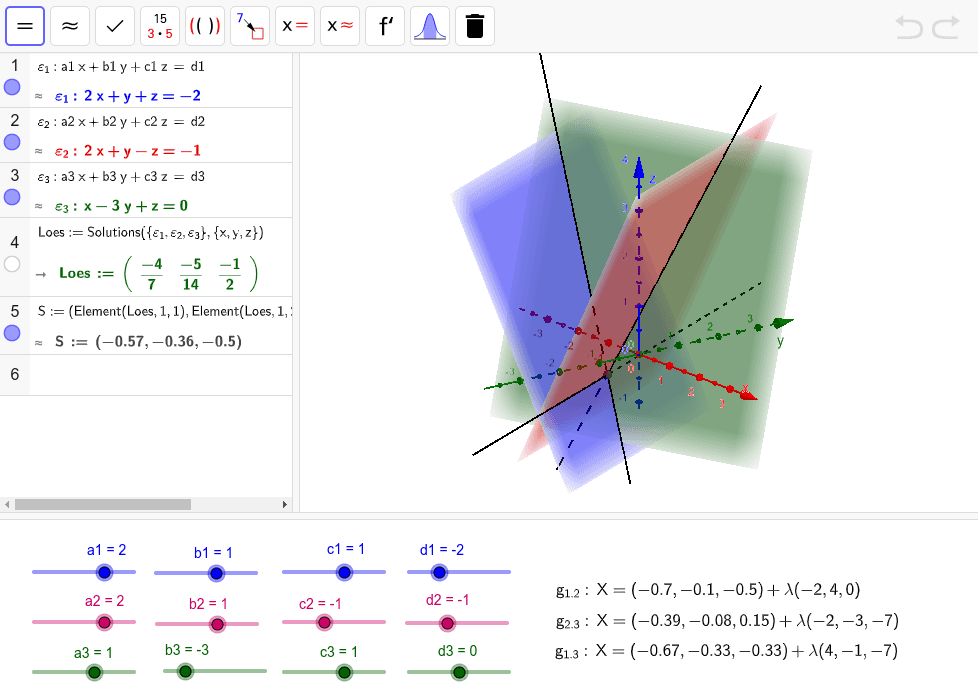
Intersection Of Three Planes Geogebra

Intersections Of Three Planes Part 1 Youtube
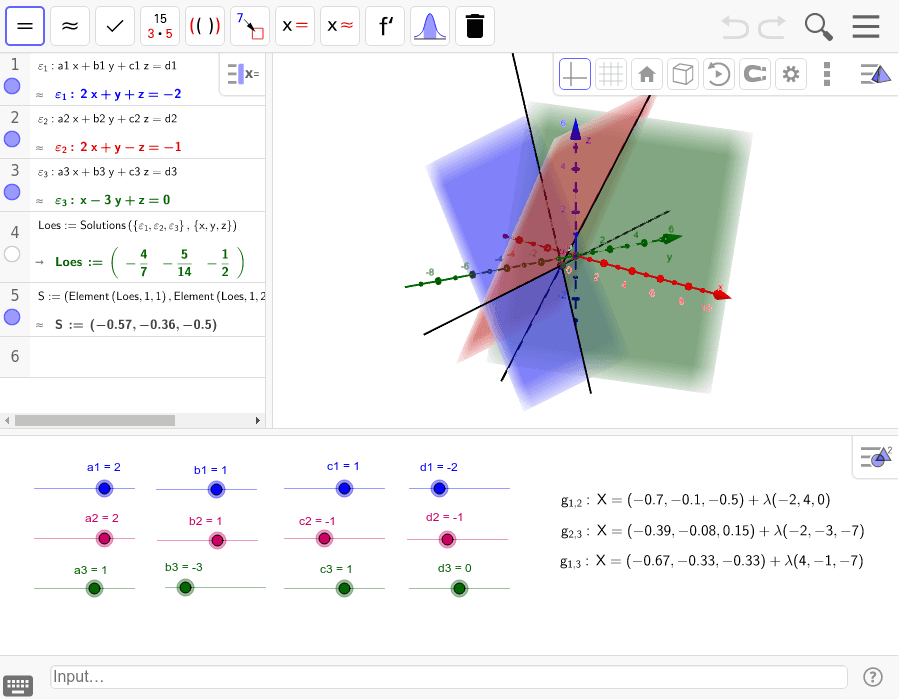
Intersection Of Three Planes Geogebra

3d Coordinate Geometry Intersection Of Planes Brilliant Math Science Wiki
Systems Of Equations In Three Variables Boundless Algebra

Lesson 84 Intersection Of 3 Planes Ppt Download

Find Variables P And Q So That 3 Planes Intersect In A Line Row Echelon Form Youtube

Lesson 84 Intersection Of 3 Planes Ppt Download

Find Variables P And Q So That 3 Planes Intersect In A Line Row Echelon Form Youtube


Posting Komentar untuk "3 Planes That Intersect In One Line"